📝 题目描述
题目链接:盛最多水的容器
给定一个长度为 n 的整数数组 height 。有 n 条垂线,第 i 条线的两个端点是 (i, 0) 和 (i, height[i]) 。
找出其中的两条线,使得它们与 x 轴共同构成的容器可以容纳最多的水。
返回容器可以储存的最大水量。
说明: 你不能倾斜容器。
示例:
1
2
3
4
5
6
7
8
9
10
11
12
13
|
示例 1:
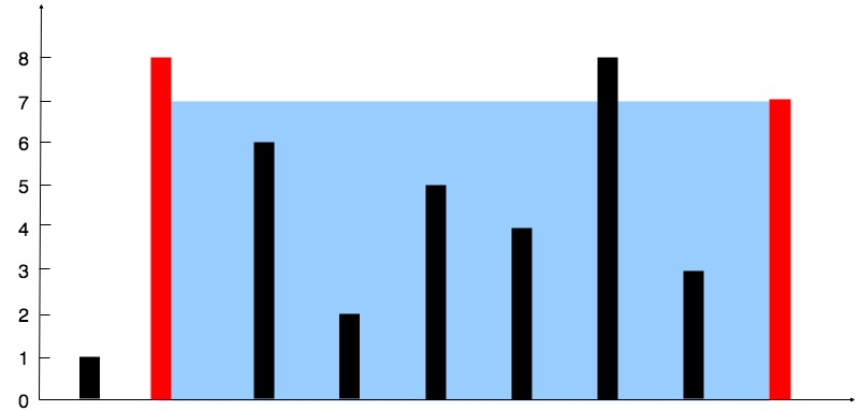
输入:[1,8,6,2,5,4,8,3,7]
输出:49
解释:图中垂直线代表输入数组 [1,8,6,2,5,4,8,3,7]。在此情况下,容器能够容纳水(表示为蓝色部分)的最大值为 49。
示例 2:
输入:height = [1,1]
输出:1
|
提示:
n == height.length2 <= n <= 10^50 <= height[i] <= 10^4
💡 解题思路
方法一:双指针
难点在于如何想到初始时让左右指针分别处于两端,然后不断让左右指针中,高度较小的那个往中间移动。
假设初始时,左指针和右指针指向的数分别为 L 和 R,假设 L≤R。同时,两个指针之间的距离为 t。那么,它们组成的容器的容量为:
min(L,R)∗t=L∗t
如果保持左指针的位置不变,那么无论右指针在哪里,都会因为左指针高度的限制,导致短板永远小于等于L,进而可以得出结论:这个容器的容量不会超过 L∗t。
比如:
向左移动右指针,指向的数为 R1,两个指针之间的距离为 t1,那么显然有 t1<t,并且 min(L,R1)≤min(L,R):
- 如果 R1≤R,那么 min(L,R1)≤min(L,R);
- 如果 R1>R,那么 min(L,R1)=L=min(L,R)。
因此有:
min(L,R1)∗t1<min(L,R)∗t
🔧 代码实现
1、双指针
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
| class Solution {
public:
int maxArea(vector<int>& height) {
int left = 0, right = height.size() - 1;
int res = 0, temp = 0;
while(left < right){
temp = (right - left) * (min(height[right], height[left]));
res = max(temp, res);
if (height[left] < height[right]){
left++;
}else{
right--;
}
}
return res;
}
};
|
📊 复杂度分析
- 时间复杂度:O(N),双指针总计最多遍历整个数组一次。
- 空间复杂度:O(1),只需要额外的常数级别的空间。
🎯 总结
